




| 09:00-10:40 | Tu1: Transport in electronic devices |
| 10:40-11:20 | Coffee break |
| 11:20-13:00 | Tu2: Surface diffusion and migration |
| 13:00-15:30 | Lunch break (on your own) |
| 15:30-16:40 | Tu3: Chemistry and growth of graphene |
| 16:40-17:20 | Coffee break |
| 17:20-18:50 | Tu4: Electron-phonon coupling in graphene |
| 19:00-21:30 | Poster session A |
Chair: W. Widdra, Halle, Germany
Contributed talk
Terahertz optical modes of supported graphene bilayer
1Dipartimento di Scienze Fisiche, Informatiche e Matematiche dell'Università di Modena e Reggio Emilia, V. Campi 213/a 41125 Modena, Italy
2CNR-Nanoscience Institute, S3 Center, 41125 Modena, Italy
3Dipartimento di Fisica, Universitá della Calabria, 87036 Arcavacata di Rende (Cs), Italy
The peculiar and promising thermal properties of graphene are strongly influenced by interactions with the substrate, presence of defects and lattice distortions. At low temperature, thermal capacity and conduction are mainly related to the properties, i.e. dispersion and density of states, of the acustic modes. The ability to tune these modes can therefore open the way to a fine control on the thermal properties of graphene-based systems, through the so-called phonon engineering [1]. Moreover, ultra-low frequency vibrations could have interesting applications such as the design of novel electromechanical nanoresonators operating in the THz range [2].
In this work, we investigate by HREELS the vibrational properties of a graphene bilayer, grown on the Ru(1000) surface (BLG@Ru) [3], unraveling the details of phonon dispersions in the THz region.
As shown in the inset of Fig. 1 a typical HREEL spectrum is built by several peaks, observed in both loss and gain sides. Spectra are fitted with a sum of gain-loss Voigt doublets, thus allowing a precise determination of the peak energy. In Fig.1 the dispersion curves are shown and compared with the theoretical dispersion of the freestanding bilayer of graphene (BLG) [4]. In the BLG case, the ZA branch splits, giving origin to the optical mode ZO', i.e. a breathing mode of the two layers [4,5]. Moreover, the TA and LA modes are expected to give origin to an optical ultra-low frequency shear mode [6,7]. In the case of BLG@Ru, we observe three optical modes, which near the Γ point are located at 4.7 (38), 8.2 (66) and 12.5 (101) meV (cm-1), respectively. Interestingly, these modes survive also at higher momentum, displaying little dispersion. These findings can be rationalized taking into account the role of the mismatch-induced layer corrugation on the phonon dispersions. In particular, the coexistence of nano-regions characterized by different interlayer distances could explain both the splitting of the optical branches and their partial localization.
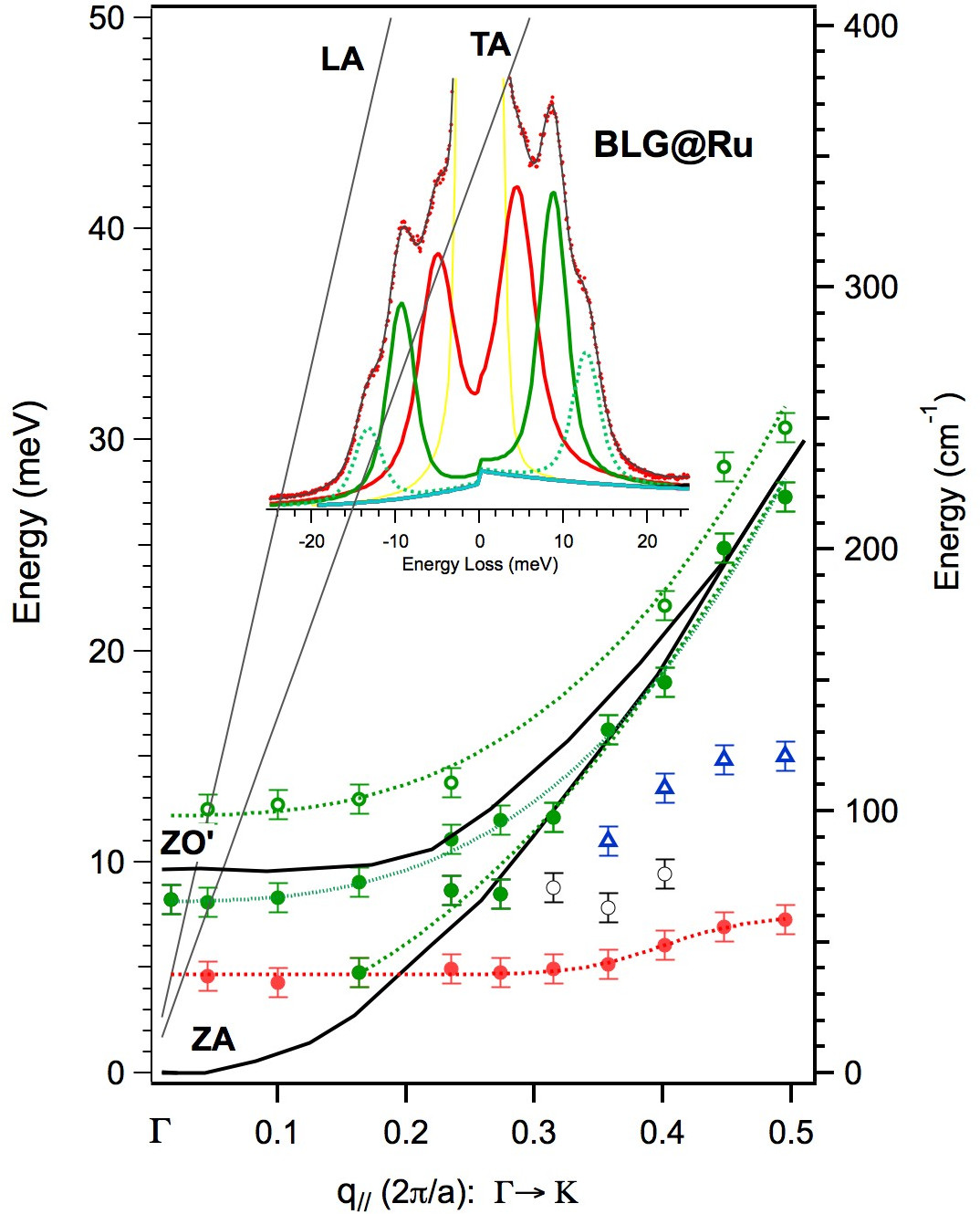
Figure 1: Phonon dispersion curves of BLG@Ru (open and filled symbols). The dotted lines are guidelines for the eyes. The solid-line black curves represents the free BLG dispersions [4]. In the inset, a typical HREELS spectrum is displayed, together with the fitting curves.
[1] E. Pop, V. Varshney, and A. K. Roy, MRS Bulletin 37, 1273 (2012)
[2] J. S. Bunch, A. M. van der Zande, S. S. Verbridge, I. W. Frank, D. M. Tanenbaum, J. M. Parpia, H. G. Craghead, P. L. McEuen, Science 315, 490–493 (2007)
[3] P. W. Sutter, J. I. Flege, E. A. Sutter, Nat. Mater. 7, 406 (2008)
[4] J.-A. Yan, W. Y. Ruan, and M. Y. Chou, Phys. Rev B 77, 125401 (2008)
[5] P. T. Araujo, D. L. Mafra, K. Sato, R. Saito, J. Kong and M. S. Dresselhaus, Sci. Rep. 2, 1017 (2012)
[6] P. H. Tan et al., Nat. Mater. 11, 294 (2012)
[7] C. Cong and T. Yu Nat. Comm. 5, 4709, 201