Poster

Exploring the electron induced phonon linewidths of N₂ on the Fe(110) surface: AIMDEF vs. DFPT

D. Novko¹, M. Blanco-Rey^1,2, J. I. Juaristi^1,2,3, and M. Alducin^1,3

¹Donostia International Physics Center (DIPC), Paseo Manuel de Lardizabal 4, 20018 Donostia-San Sebastián, Spain

²Departamento de Física de Materiales, Facultad de Químicas UPV/EHU, Apartado 1072, 20080 Donostia-San Sebastián, Spain

³Centro de Física de Materiales CFM/MPC (CSIC-UPV/EHU), Paseo Manuel de Lardizabal 5, 20018 Donostia-San Sebastián, Spain

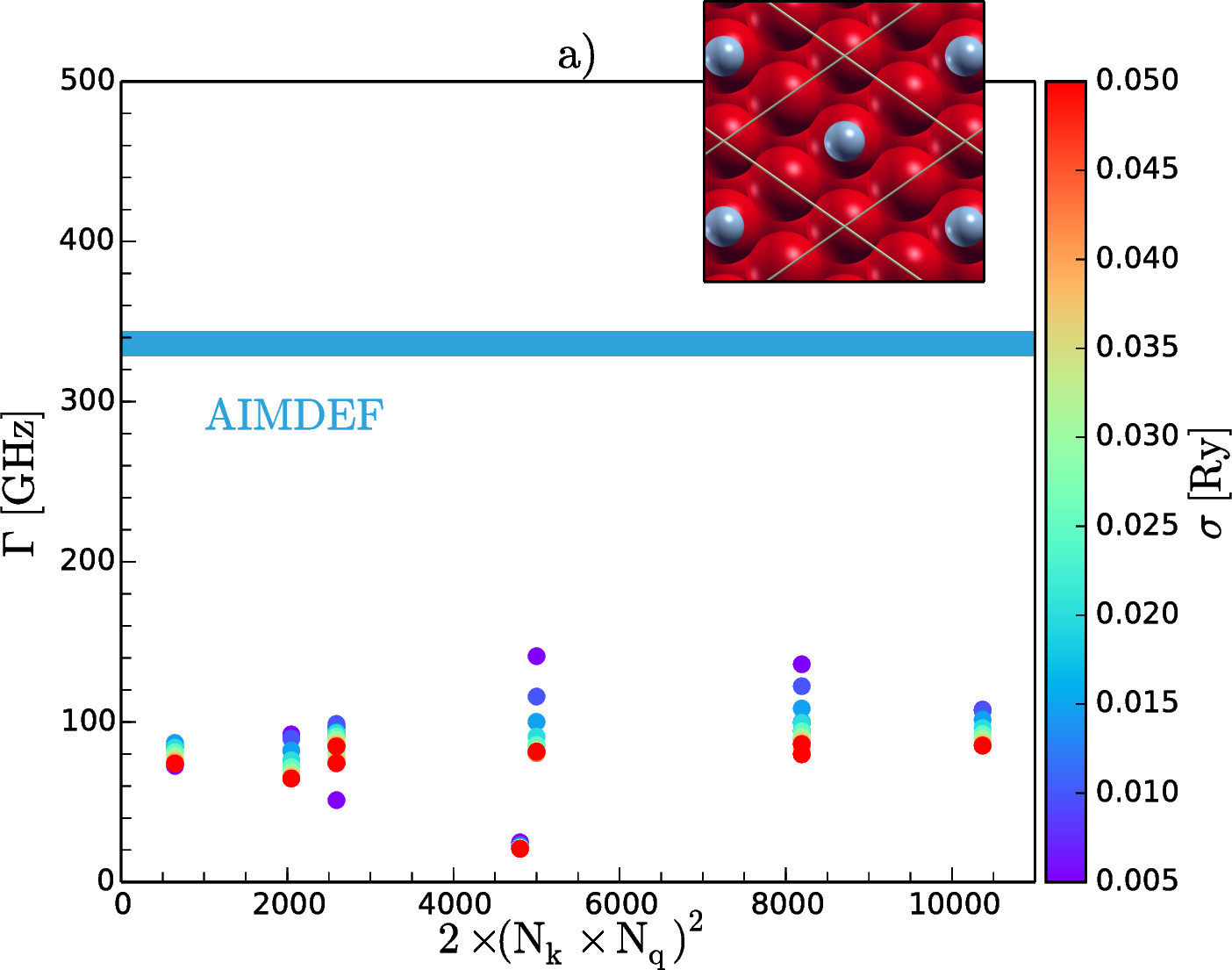
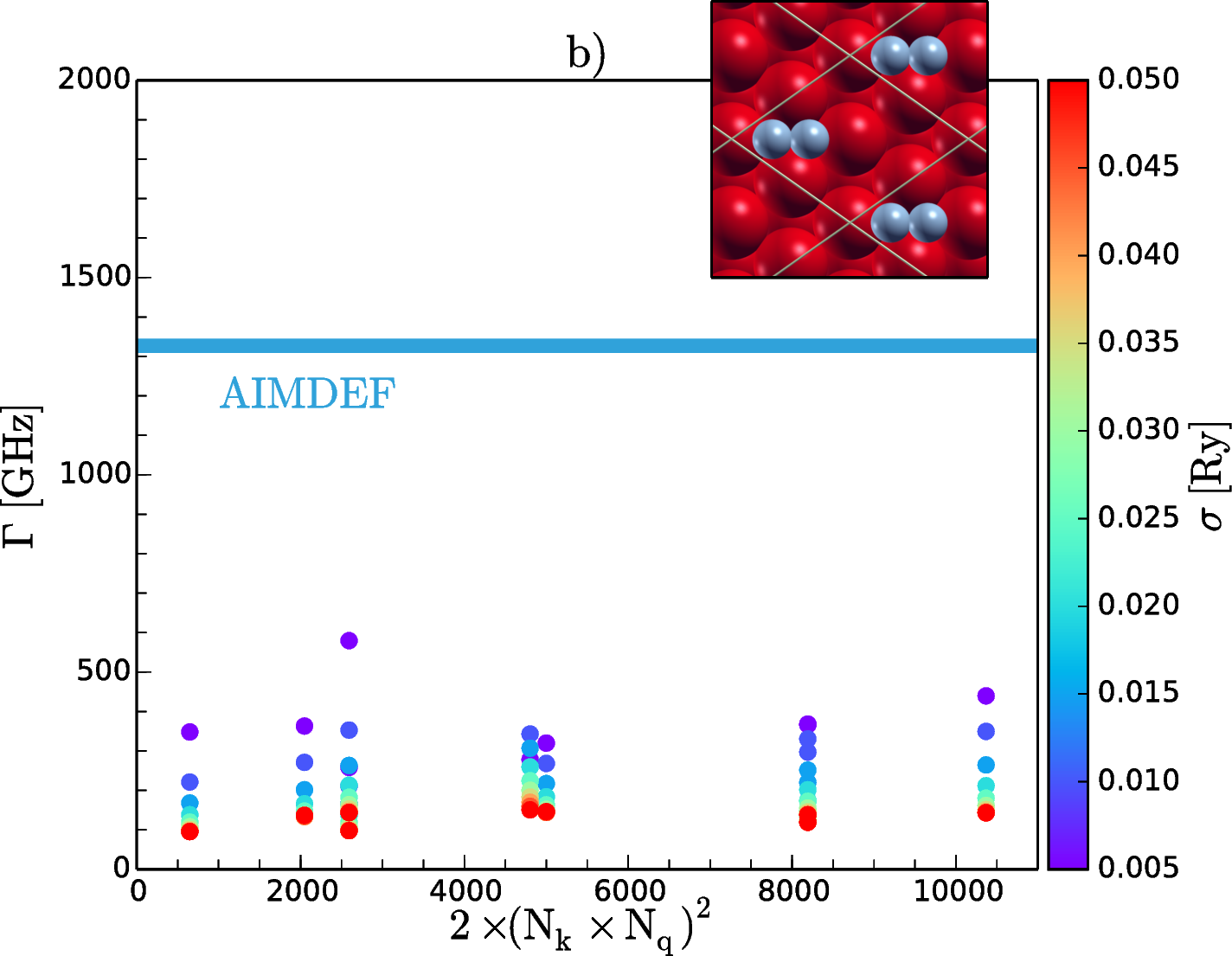
To properly describe gas/surface dynamics it is crucial to understand the non-adiabatic effects that come from the energy exchange between the ionic degrees of freedom of the adsorbates and the electronic continuum of the surface. One way to account for this electron-hole (e-h) pairs excitation is to incorporate an electronic friction term into the classical equations of motion within the local density friction approximation (LDFA) [1]. Ab initio molecular dynamics (AIMD) together with this approximation (AIMDEF) [2] constitutes a very useful tool to explore the vibrational relaxation of an adsorbate on a metal surface. Using this method we calculated the e-h pair induced linewidths, Γ, of N₂ vibrating on top (Fig. 1a) and hollow (Fig. 1b) sites of a Fe(110) frozen surface. To make a comparative study we also performed density functional based perturbation theory (DFPT) calculations within the quasi-static limit (i.e. the limit of small vibrational frequencies) [3]. Although we get different values for the two methods, they both agree that phonon linewidth for internal stretch mode of N₂ on the hollow site is larger than on the top site.

Figure 1: Phonon linewidths, Γ, of the internal stretch mode when N₂ is adsorbed vertically on the top (a) and horizontally on the hollow (b) sites of Fe(110). The abscissas represent the number of electronic transitions across the Fermi level considered in different samplings of the surface Brillouin zone and σ represents the broadening parameter of the initial and final state energies used in DFPT method.

[1] J. I. Juaristi et al., Phys. Rev. Lett. 100, 116102 (2008)

[2] M. Blanco-Rey et al., Phys. Rev. Lett. 112, 103203 (2014)

[3] B. Hellsing and M. Persson, Phys. Scr. 29, 360 (1984)