Poster
Modelling of STM-induced diffusion of hydrogen interstitials in the Pd(111) near-surface region
1Departamento de Física de Materiales, Facultad de Químicas, Universidad del País Vasco UPV/EHU, Apdo. 1072, 20080 Donostia-San Sebastián, Spain
2Donostia International Physics Center, P. Manuel de Lardizabal 4, 20018 Donostia-San Sebastián, Spain
3Institute for Chemistry and Biochemistry, Freie Universität Berlin, Takustrasse 3, 14195 Berlin, Germany
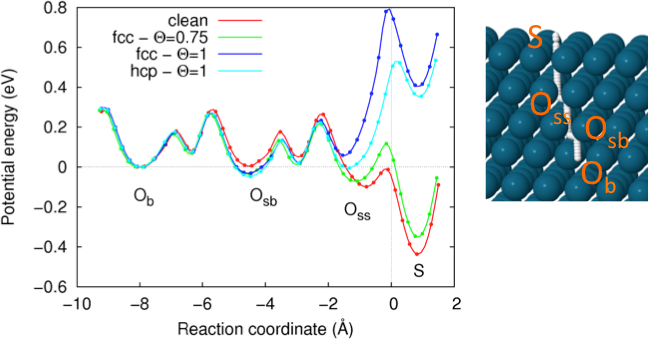
STM experiments have shown that it is possible to manipulate buried [1] and adsorbed [2] H on Pd(111) to produce nanopatterned surface structures of PdHx composition. Although the experimental observations point to occupation of the subsurface sites (Oss), the actual distribution of H in the manipulated regions is unknown. The factors determining the diffusion of H are: inelastic collisions with STM electrons, H-H interactions, and tip effects in the form of electrostatic fields. We have studied these three factors first at a static level, by DFT evaluations of the potential energy surface (PES) of a H interstitial at the surface region [3], and then at a dynamical level. In the latter, we use a new quantum-mechanical model of the non-adiabatic coupling (NAC) between the H vibrational states with their metallic embedding electron density, which accounts for the electronic structure details of the Pd Fermi surface [4]. The static study rules out significant electrostatic effects for typical STM bias voltages, V < 2 V, but shows that H precoverage strongly modifies the PES around the Oss site (see Figure). Surface, S, sites are energetically favoured by 280-340 meV and resurfacing is likely whenever empty S sites are available, with barriers < 200 meV. The NAC model for H transfer rates evidences this strong preference for resurfacing of buried interstitials for voltages and tunnelling intensities up to V = 1 V and I = 1 nA, respectively. It also shows that at saturation Oss sites are also depopulated towards deeper sites. Most importantly, at long times (~100 ns) the system behaves quasi-thermally, and the site population dynamics can be described in terms of effective equilibrium constants.

Figure 1: One-dimensional PES for H in the near-surface region of Pd(111) for surface site coverages Θ= 0-1.
[1] E. C. H. Sykes et al, PNAS 102, 17907 (2005)
[2] T. Mitsui et al, Angew. Chem. Int. Ed. 46, 5757 (2007)
[3] M. Blanco-Rey and J. C. Tremblay, J. Chem. Phys. 142, 154704 (2015)
[4] J. C. Tremblay and M. Blanco-Rey, Phys. Chem. Chem. Phys. (in press)